🧮 The Maths behind Bayes’ Theorem and The Resurrection

(This is an addendum to the main essay found here. 다시 원 에세이로 가려면 여기.)

Let’s walk through the main calculation, adding a few details to account for N independent eyewitnesses. Even if you’re not mathematically inclined, I believe this exercise will help you appreciate key aspects of the process we use every day: how we constantly update our prior beliefs in light of new evidence, the exponentially powerful impact of multiple independent witnesses, and the importance of keeping an open mind—namely, not setting prior probabilities to zero. As long as the prior probability, no matter how small, is greater than zero, the overwhelming weight of independent, credible testimonies will easily shift the belief towards a more evidence-driven conclusion, regardless of how improbable the event seemed at first. This is the power of Bayesian reasoning—showing that evidence can truly reshape our understanding, even when starting from a low prior. 

Formulation of Bayes’ Theorem

First, let’s define some terms:

• P(M) represents the prior probability (or, if you prefer, your initial belief or presupposition) that a miracle M happened. In this case, we’re talking about the resurrection of Jesus on the third day.
• P(M|O) is the posterior probability, or the updated belief about the miracle M, given the evidence O (such as eyewitness testimonies).
• P(O) is the overall probability of the evidence O occurring. This is a crucial factor because it helps properly normalise the overall probability and bring us to the posterior probability.
• P(O|M) is a more challenging concept, but it is essential to understanding Bayes’ Theorem. It refers to the likelihood of the evidence (the eyewitness testimonies) assuming that the resurrection actually happened. This is how probable the testimonies are, given that the event occurred.

Baye’s Theorem itself states that:

The posterior probability of Jesus’ resurrection, given the eyewitness testimonies, is equal to the (appropriately normalised) probability of those testimonies being true assuming the resurrection happened, multiplied by the prior probability that a supernatural event like the resurrection could occur. 

This is written mathematically as:

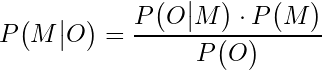
Now, we can express the denominator as:

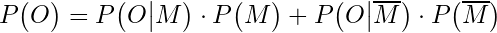
With some rearranging, we can simplify the expression for the posterior probability to:

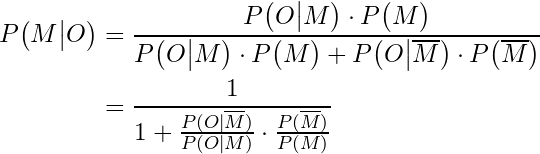
At this point, the formula may look a bit complicated, but don’t worry—it boils down to two key ratios:

1. The ratio of prior probabilities: the probability of the resurrection being real versus not real.
2. The ratio of likelihoods of the evidence: how likely the eyewitness testimonies are, assuming the resurrection happened versus assuming it didn’t.

Let’s focus on the first ratio. The key point here is the importance of keeping an open mind. This means we don’t assume a prior probability of zero for miracles, no matter how unlikely they might seem. In mathematical terms:

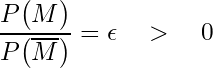
In simpler terms, this means we assign a non-zero probability to the resurrection being possible.

It’s worth briefly noting that, in light of the advancements in quantum mechanics over the last century, this non-zero prior probability isn’t just reasonable—it’s actually in keeping with the current understanding of the universe. Quantum theory teaches that nothing is strictly “impossible”—only “improbable.” By this logic, to dismiss miracles outright by setting their prior probability to zero contradicts the very principles of modern science, where probabilities govern all phenomena, even those that might seem extraordinary.

Multiple Independent Eyewitnesses

Now let’s focus on the second ratio. How can we incorporate the testimonies of N independent eyewitnesses into our calculation?

To do this, we need to apply a key rule of probability, known as the multiplication rule for independent events. This rule states:

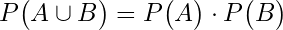
In simple terms, it says that the probability of two independent events—A and B—both occurring is the product of their individual probabilities.

Now, let’s extend this concept to N independent eyewitnesses. The probability of all N eyewitnesses independently corroborating the miracle (i.e., witnessing the resurrection) is the product of the probabilities of each individual testimony. Mathematically, we write this as:

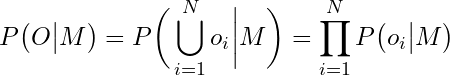
This equation shows how we multiply the probabilities of each eyewitness testimony to find the overall likelihood of the evidence, assuming the resurrection occurred.

With this, we can now re-write the ratio of likelihoods from earlier:

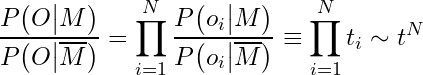
Here, t represents the average trustworthiness of an independent eyewitness. In this context, trustworthiness is defined as the ratio of two probabilities: the probability that an eyewitness would report having seen the resurrection, assuming the resurrection actually occurred, versus the probability that an eyewitness is falsely claiming to have seen it, assuming the resurrection did not happen.

For the average person, who is not a sociopath or psychopath, we can reasonably expect this t value to be greater than 1. This reflects the idea that most people are generally truthful and would not invent such a testimony unless they had genuinely experienced it.

Putting it together, the expression for our posterior probability now reads:

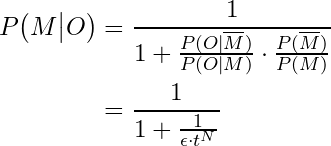
Let’s now follow in the footsteps of Charles Babbage, the father of computing, and calculate some key probabilities involved in evaluating the evidence for the resurrection. We’ll use numerical approximations to estimate the likelihood of Jesus’ resurrection based on the principles of Bayes’ Theorem. To do this, we need to make educated guesses about three main factors:

• t = 2.  This represents the “trustworthiness” of an individual eyewitness, on a scale where 1 would mean total uncertainty (essentially no trust) and anything above 1 indicates reliability. Here, we’ll use 2 as a very conservative estimate, meaning we are assuming each eyewitness is, on average, twice as likely to be truthful than not. This is a modest estimate—given the nature of the event and the character of the people involved, this number could easily be higher.
• N = 500. The number of independent eyewitnesses. We base this on the scriptural record, particularly 1 Corinthians 15:6, which states that more than 500 people saw Jesus alive after His resurrection. This isn’t just a handful of witnesses, but a large group of people, all at the same time, all reporting the same event. A side note: the idea of mass hallucinations occurring in such a large group at once is not only highly implausible but, as far as we know, has never been documented in human history.
• ε = 10^-100. This is the prior probability, which serves as our starting point for the calculation. It represents how likely we initially believe a supernatural event, like the resurrection, is to occur. 10^-100 is an unimaginably small number—far smaller than anything we would encounter in everyday life. To put it in perspective, this is the probability of randomly selecting the exact atom in a whole galaxy cluster. Yet, it’s still not zero. The key point here is that even though this prior probability is astronomically small, it’s not so small that we rule out the possibility completely. As long as it’s not zero, the additional evidence (such as eyewitness testimony) can still have an impact on our final conclusion.

In fact, it’s worth briefly noting that, in light of recent advancements in quantum mechanics, this non-zero prior is not only reasonable, but also aligns with modern scientific thinking. Quantum theory has taught us that nothing is strictly “impossible”—only “improbable.” Events that seem extraordinarily unlikely can still happen, and probabilities govern all phenomena, even those that defy our intuitions. This stands in stark contrast to what David Hume did in his essay On Miracles, where he effectively set the prior probability for miracles to zero, dismissing them outright as impossible. Hume’s approach, in which he arrogantly closed the door on any possibility of the supernatural, reflects a profound ignorance of the very nature of probability and scientific inquiry. By setting the prior to zero, he not only ignored the potential for new evidence to shape our beliefs but also contradicted the principles of modern science itself. In contrast, by leaving the prior non-zero, we allow room for the evidence—like credible eyewitness testimony—to update our beliefs in a way that aligns with both reason and scientific understanding.

Now, let’s do the math. First, we calculate the contribution of the eyewitnesses using the formula  t^N :

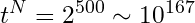
The impact of independent testimonies grows exponentially—10 to the power of 167—illustrating how their combined strength amplifies in an overwhelmingly powerful way.

Now, using Bayes’ Theorem, we can calculate the posterior probability, which tells us how likely the resurrection is, given the evidence. This is written as:

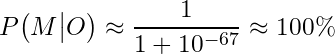
This approximation shows that the posterior probability of the resurrection is virtually 100%, or 99.99999… with 65 nines after the decimal! In other words, once we update our prior belief with the overwhelming evidence of 500 independent eyewitnesses who all testified to seeing the risen Jesus, the probability that the resurrection actually happened skyrockets.

Having gone through an entire Bayesian calculation process from the beginning to the end, I hope now that you will better appreciate key aspects of the process we use everyday: how we constantly update our prior beliefs in light of new evidence, the exponentially powerful impact of multiple independent witnesses, and the importance of keeping an open mind—namely, not setting prior probabilities to zero. As long as the prior probability, no matter how small, is greater than zero, the overwhelming weight of independent, credible testimonies will easily shift the belief towards a more evidence-driven conclusion, regardless of how improbable the event seemed at first. This is the power of Bayesian reasoning—showing that evidence can truly reshape our understanding, even when starting from a low prior.

(Click here to go back to the main essay.)
(한글 에세이로 다시 가시려면 여기로.)